A partir de la CdeR2008 se introdujeron en las cuentas nacionales las mediciones reales en mediciones reales encadenadas, obtenidas a partir de una base de precios móvil. Esta metodología es ampliamente aplicada a nivel internacional, dado que utiliza los precios del año anterior para valorar las cantidades del año en curso, permitiendo utilizar estructuras de precios relativos continuamente actualizadas y no las estructuras de precios relativos de un año fijo, pues estas van perdiendo gradualmente representatividad a través del tiempo, distorsionando las mediciones en términos reales. La base móvil lleva a una constante actualización de las estructuras de los distintos agregados de oferta y utilización que componen el PIB, de manera que la medición del crecimiento de dichos agregados sea lo más precisa y fiable posible.

En términos generales, el proceso para elaborar las cuentas nacionales en términos reales comprende dos etapas. La primera consiste en obtener medidas de volumen en base móvil, para lo cual se elaboran índices de Laspeyres valorados a precios promedio del año anterior, denominados eslabones para fines de este ejercicio. La segunda etapa consiste en encadenar dichos índices o eslabones.

Base móvil

Las medidas en base móvil o eslabones se construyen en base a la formulación del índice de volumen de Laspeyres, donde las cantidades del año corriente valoradas al precio promedio ponderado del año anterior²³, se expresan en razón de las cantidades y precios del año anterior:

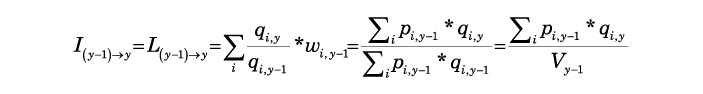
siendo,

L_(y-1)->y : Índice de volumen de Lasperyres que mide la variación en el volumen entre período y-1 e y, con el período y-1 como período base de referencia

p _{i, y-1} : precio del rubro i en el período y-1

q_{i, y} : cantidad del rubro i en el período y

w _i,y-1 : ponderación proporcional del período base , es decir la proporción del rubro en el valor total del preríodo y-1

V_y-1 : valor total a precios corrientes en el período y-1

Tanto en el caso de las CNA como de las CNT, los eslabones se construyen utilizando el precio promedio ponderado del año anterior. Es decir, las cantidades del año o trimestre corriente se valoran al precio promedio del año anterior, y se expresan en razón de las cantidades y precios promedio de dicho año.

La mayoría de los países que calculan medidas de volumen encadenado utilizan los índices de Laspeyres para elaborar los eslabones, entre otras razones por la coherencia que se asegura entre los índices trimestrales encadenados y el respectivo índice anual. Este es un argumento adicional para realizar el encadenamiento con frecuencia anual, ya que la congruencia entre los datos trimestrales y los índices anuales requiere que en las CNT y las CNA se utilicen las mismas ponderaciones de precios y, en consecuencia, que las CNT sigan la misma práctica de cambio de año base/encadenamiento que las CNA.

Encadenamiento de los eslabones

Los eslabones obtenidos en la etapa anterior son encadenados considerando como referencia el año anterior.

En el caso de las CNA, la serie de índices encadenados se obtiene como la multiplicación sucesiva de los eslabones anuales. El índice encadenado de un determinado año es igual al producto de los eslabones desde el origen de la serie hasta dicho año, o equivalentemente, a la multiplicación del índice encadenado del año anterior por el eslabón del año corriente. Esto es:

donde,
IE_0⟶y : es el índice encadenado entre el periodo 0 e y.

I_(t-1)⟶r :es el índice de volumen que mide la variación entre el periodo t-1 y t.

Las tasas de crecimiento de las medidas en base móvil anual, respecto de sus niveles de referencia, son las mismas que las tasas interanuales del índice encadenado. Es decir, el proceso de encadenamiento no altera la evolución interanual del índice base móvil.

La equivalencia entre las tasas de variación de las mediciones en base móvil y las de la serie de índices encadenados, permite el cálculo de incidencias aditivas de los componentes de los agregados macroeconómicos.

En el caso de las CNT, el encadenamiento se ve afectado por los componentes estacionales de las series, lo cual puede llevar a que los resultados del encadenado anual no sumen los encadenados trimestrales. Para subsanar este problema, en las estimaciones de los índices trimestrales se utilizan precios promedios anuales para el cálculo de la estructura de ponderaciones.

Existen tres técnicas de encadenamiento en función del período usado como referencia: solapamiento anual, solapamiento a un trimestre y solapamiento trimestral. Las tres técnicas consideran como ponderadores los precios promedios del año anterior; la diferencia radica en las cantidades comparadas. El solapamiento anual considera las cantidades promedio del año anterior; el solapamiento a un trimestre, las de un trimestre del año anterior (generalmente el cuarto); y el trimestral, compara las cantidades del trimestre actual con las del mismo trimestre del año anterior. Para las mediciones en términos de volumen, en Chile se utiliza el método de solapamiento anual, debido a que en las medidas de volumen tipo Laspeyres los datos trimestrales son aditivos con el correspondiente índice anual, lo que constituye una ventaja importante para el análisis²⁴.

En el caso particular de las CNT y dado que la técnica elegida es el solapamiento anual, el encadenamiento es similar al anual, con la única salvedad que cada trimestre en base móvil se extrapola con respecto al índice promedio y no con respecto a igual trimestre del año anterior. Este método asegura que el encadenamiento anual coincida con el promedio de los índices encadenados trimestrales²⁵.

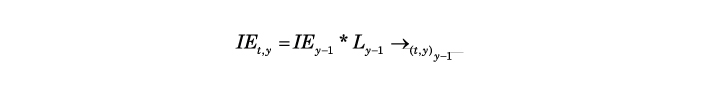
siendo  índice trimestral de Laspeyres a corto plazo o eslabón de trimestre t del año y.

Presentación de los datos

De acuerdo a lo revisado en los puntos anteriores, las CNA y CNT se publican en niveles a precios corrientes y de volumen a precios del año anterior encadenado, incluyendo las tasas de variación interanuales y contribuciones a la tasa de variación del PIB. De la misma forma se publican las mismas series, nominales y de volumen, ajustadas por estacionalidad y efecto calendario²⁶.

Los niveles de las series de volumen a precios del año anterior encadenados son presentados en términos monetarios, lo cual corresponde a la multiplicación del índice encadenado promedio del año 2018 por el valor nominal de la serie para el año de referencia (en este caso, 2018).

La utilización de la metodología de encadenamiento presenta el problema de la no aditividad. Esto significa que las series de los agregados macroeconómicos a precios del año anterior encadenado expresados en términos monetarios no corresponden a la suma de sus componentes. Solo los dos primeros años de las mediciones encadenadas mantienen la propiedad aditiva, ya que estas son equivalentes a las mediciones en base móvil de esos años, las que si son aditivas. Ejemplo de ello se puede observar en el PIB por origen, el cual no corresponde a la suma de las actividades, o el consumo privado que también difiere de la suma de sus componentes.

Considerando la no aditividad de las series encadenadas, se publican contribuciones aditivas al crecimiento del PIB tanto de las series anuales como trimestrales²⁷.

La presentación de las cuentas nacionales trimestrales detallada en esta sección se ajusta a la experiencia internacional respecto de la publicación de series encadenadas, así como también a las recomendaciones propuestas por el FMI en el Manual de Cuentas Nacionales Trimestrales²⁸ y por otros organismos internacionales como la OCDE y Eurostat.